Keeping up with my exercise regime I went swimming this lunchtime. Alas length swimming was done to one lane as there was an aqua class going on meaning swimmers of all standards are in one narrow channel and being the slowest I was conscious of getting in other people's way. But I plodded on regardless and managed a full 30 minute swim. I used my tried and tested method of thinking of the bloke from Touching The Void, (or Touching-the-void-o as I call him in my head, because as impressed with him as I am that doesn't go as far as me looking him up to find his real name) who crawled down a mountain with a broken leg. If he could do that my internal argument goes, then however tired I am I can do another minute or two. Using this technique a few times you can double your workout. Thanks Touching-the-void-o. And yes, what I did today is comparable to what you did.
One of the slightly weird things for me about the pool I go to is that one of the members of the aqua class is my childhood (and let's face it adulthood) crush Janet Ellis, from off of Jigsaw. How bamboozled the teenage me would be if he knew that one day he would be semi-naked only inches away from a semi-naked Janet Ellis, that water that had touched my semi-naked body would also touch hers? I don't know. But I am bamboozled when I think about it now. I am a gentleman and although I am now friends with Janet I never say hello to her when I am swimming. A lady does not like to be acknowledged in aqua-classes. She says nothing either, though I know she has seen me, thinking about our semi-nakedness, because she mentioned in a radio interview that it annoys her that I don't tie my hair back when I am swimming. She doesn't like my long hair trailing in the water. But it's a lot less disgusting than what's going on in my head.
Today though I was amused to note that one of the songs played by the aquaclass leader was by Sophie Ellis-Bextor, Janet's daughter, which must have been slightly odd for her. Indeed she later tweeted asking what the etiquette for such a situation should be. Then again I was worrying about the etiquette of what one should do when a molecule of water that had previously been inside my swimming trunks was now touching the very chest area that I had quietly obsessed about thirty years before. It's a strange and perverse world.
Later I carried some heavy shopping home the mile of so from Hammersmith. The bags were cutting into my hand and I wanted to put them down. But I thought of Touching-the-Void-o and managed to carry on to my goal. It's a great exercise tip. Also have your childhood crush in the swimming pool so you feel the need to impress them by not giving up too fast. All these are good tips. Keep reading the blog for more.
You have to love my geeky readers. I got an email from someone calling themselves, "Bradlaugh's Finger" (a reference to the statue of the founder of the National Secular Society in Northampton?) who has some interesting news for other nerds (it may confound normal people, but there are none of them reading this). Here's his email:
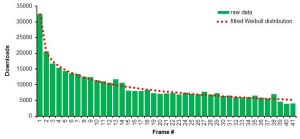
"Turns out your snooker download data are well approximated by a Weibull distribution with shape parameter 0.3643 and scale parameter 7.53751. This fits the data very well indeed, with a coefficient of determination of 0.981 (where 1 would be a perfect fit).
Weibulls are commonly used to model survival (e.g. of people who might die, or of components that might fail in a system). The fact that the shape parameter is less than 1 means that, although the decline is inexorable, the rate of attrition reduces as time extends -- at each successive timepoint, the proportion of individuals from the last timepoint leaving the population will decrease. In the words of that wikipedia article, 'This happens if there is significant "infant mortality", or defective items failing early and the failure rate decreasing over time as the defective items are weeded out of the population.'
This gives us a model with which to extrapolate into the future: a continuous probability distribution like this never reaches zero but, if the trend continues, the expected number of downloads is due to drop below 1 in frame 4,653. Work out any number you like: the number of downloads you can expect for frame x is exp(-(((x-1)/7.53751)^0.3643)) * 32463
Peace / BF"
And proof that the recession is hitting me hard was found by comedian Matt Kirschen. His photo clearly shows that I've been forced to start selling slices of myself off for $2.99. Tuck into that. Nyum, nyum, nyum.
You can read all my latest news in the January Newsletter - you can subscribe and get these montly to your inbox by filling in the box at the top of the page.